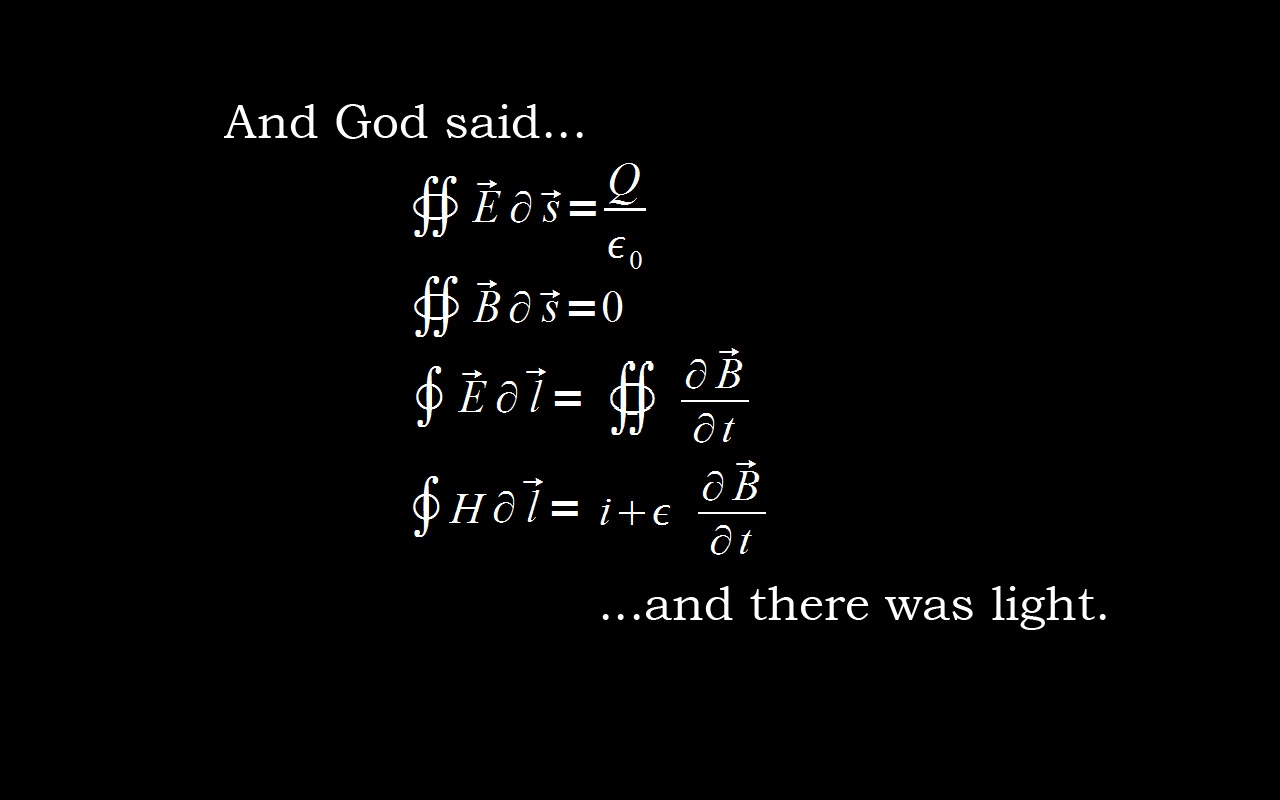
麦克斯韦方程组可以算得上是物理学史上最优美的一组方程了，就像镇楼图里说的那样，因为麦克斯韦方程组，所以才有了光。

麦克斯韦方程组积分形式的推导和证明

高斯定律

高斯定律表示任意曲面的电通量之和等于其中包含的电荷数，证明了电场是有源场

推导方式如下：

根据库仑定律及电场强度的定义，空间内某一点出电场强度为：

$$ \vec{E} = \frac{q}{4 \pi \varepsilon \cdot r^2} \space \vec{e}_r $$

在空间内任取一封闭曲面，在曲面内任一点处放置一点电荷$q$，曲面电通量的微元为：

$$ d \Phi =\vec{E} \cdot d \vec{S} = \frac{q}{4 \pi \varepsilon \cdot r^2} \space dS \space cos \theta = \frac{q}{4 \pi \varepsilon} \cdot\frac{d S^{\prime}}{ r^2} $$

电通量之和为：

$$ \begin{split} \Phi & = \oint_{S} \vec{E} \cdot d\vec{S} \\\\ & = \oint_{S} \frac{q}{4 \pi \varepsilon} \cdot\frac{d S^{\prime}}{r^2} \\\\ & = \frac{q}{4 \pi \varepsilon} \cdot\frac{4 \pi r^2}{r^2} \\\\ & = \frac{q}{\varepsilon} \end{split} $$

高斯磁定律

高斯磁定律表示任意曲面的磁通量之和为零，证明了磁场是无源场

推导方式如下：

根据毕奥-萨伐尔定律：

$$d \vec{B} = \frac{\mu}{4 \pi} \cdot \frac{Id \vec{l} \times \vec{r}}{r^2}$$

曲面的磁通量为：

$$ \oint_{S} \vec{B} \cdot d\vec{S}= \frac{\mu I}{4 \pi} \oint_{S} \frac{d \vec{l} \times \vec{r}}{r^2} \cdot d \vec{S}$$

• 当电流元位于曲面内部时，$\vec{r}$与$\vec{S}$间相互平行，磁通量积分$ \oint_{S} \vec{B} \cdot d\vec{S}= 0 $
• 当电流元位于曲面外侧时，做一个包含电流元在内的辅助曲面，由增补法可得磁通量积分$ \oint_{S} \vec{B} \cdot d\vec{S}= 0 $

法拉第电磁感应定律

法拉第电磁感应定律是由实验现象归纳得到的，表明了变化的磁场产生电场

推导方式如下：

设一变化的磁场中放置一个环形线圈，回路中的电动势是电场强度的环路积分：

$$ \varepsilon = \oint_{l} \vec{E} \cdot d\vec{l} $$

同时实验表明回路中电动势等于磁通量的变化率：

$$ \varepsilon = - \frac{d \Phi}{dt} = - \iint_{S} \frac{\partial \vec{B}}{\partial t} \cdot d\vec{S} $$

综合两式可得法拉第电磁感应定律的积分形式：

$$ \oint_{l} \vec{E} \cdot d\vec{l}= - \iint_{S} \frac{\partial \vec{B}}{\partial t} \cdot d\vec{S} $$

全电流定律

全电流定律是麦克斯韦根据安培环路定理扩展了位移电流的部分而得到的
表明了电流和变化的电场产生磁场

推导方式如下：

根据毕奥-萨伐尔定律：

$$d \vec{B} = \frac{\mu}{4 \pi} \cdot \frac{Id \vec{l} \times \vec{r}}{r^2}$$

竖直导线周围某点的磁场强度为

$$ B = \frac{\mu I}{2 \pi r} $$

对任意闭合路径存在环路积分：

$$ \oint_{l} \vec{B} \cdot d\vec{l} = \oint_{l} B \space r \space d \varphi = \oint_{l} \frac{\mu I}{2 \pi r} \space r \space d \varphi = \mu I \tag{*} $$

以上标星号(*)的公式即安培环路定理

同时引入位移电流的概念：位移电流是由电场变化引起的电流变化，不产生焦耳热但仍具有磁效应，电容器极板间的充放电就是位移电流，位移电流的表达式：

$$ I_D = \mu \iint_{S} \frac{\partial \vec{D}}{\partial t} \cdot d\vec{S} $$

综合可得全电流定律：

$$ \oint_{l} \vec{H} \cdot d\vec{l}= I + \iint_{S} \frac{\partial \vec{D}}{\partial t} \cdot d\vec{S} $$

总结

一般情况下积分形式的麦克斯韦方程组如下：

高斯定律

$$ \oint_{S} \vec{D} \cdot d\vec{S}= q \tag{1} $$

高斯磁定律

$$ \oint_{S} \vec{B} \cdot d\vec{S}= 0 \tag{2} $$

法拉第电磁感应定律

$$ \oint_{l} \vec{E} \cdot d\vec{l}= - \iint_{S} \frac{\partial \vec{B}}{\partial t} \cdot d\vec{S} \tag{3} $$

全电流定律

$$ \oint_{l} \vec{H} \cdot d\vec{l}= I + \iint_{S} \frac{\partial \vec{D}}{\partial t} \cdot d\vec{S} \tag{4} \label{4} $$

由麦克斯韦方程组的积分形式推导其微分形式

Nabla算子简介

Nabla算子($\nabla$)是一种矢量算符，可以将标量场转化为梯度的矢量场，借助它及其点积、叉积能够方便地表示$梯度(grand)$、$散度(div)$、$旋度(curl)$ 等概念：

$$\nabla = \frac{\partial }{\partial x} \vec{i} + \frac{\partial }{\partial y} \vec{j} + \frac{\partial }{\partial z} \vec{k} $$

$$\nabla E = grand({E}) = \frac{\partial E }{\partial x} \vec{i} + \frac{\partial E }{\partial y} \vec{j} + \frac{\partial E }{\partial z} \vec{k} $$

$$\nabla \cdot \vec{E} = div(\vec{E}) = \frac{\partial E_x }{\partial x} + \frac{\partial E_y }{\partial y} + \frac{\partial E_z }{\partial z} $$

$$\nabla \times \vec{E} = curl(\vec{E}) = \left ( \frac{\partial E_z}{\partial y} - \frac{\partial E_y}{\partial z} \right ) \vec{i} + \left ( \frac{\partial E_x}{\partial z} - \frac{\partial E_z}{\partial x} \right ) \vec{j} + \left ( \frac{\partial E_y}{\partial x} - \frac{\partial E_x}{\partial y} \right ) \vec{k}$$

高斯定律

取空间内任一六面体的体积元，以三条棱为轴建立xyz直角坐标系。则对于任意两个相对的面，电通量之和为：

$$
\left ( \vec{D} + \frac{\partial \vec{D}}{\partial x} \right ) \cdot \vec{i} \space dydz - \vec{D} \cdot \vec{i} \space dydz = \frac{\partial \vec{D}}{\partial x} \cdot \vec{i} \space dydz = \frac{\partial D_x}{\partial x} \space dxdydz
$$

对于整个体积元来说，六个面的电通量之和为：

$$
\oint_{S} \vec{D} \cdot d\vec{S} = \left ( \frac{\partial D_x}{\partial x} + \frac{\partial D_y}{\partial y} + \frac{\partial D_z}{\partial z} \right ) dxdydz = \rho dxdydz
$$

引入哈密顿算子$\nabla$，可得微分形式如下：

$$\nabla \cdot \vec{D}=\rho$$

高斯磁定律

形式与方法与高斯电定律相同，同理可得：

$$
\oint_{S} \vec{B} \cdot d\vec{S} = \left ( \frac{\partial B_x}{\partial x} + \frac{\partial B_y}{\partial y} + \frac{\partial B_z}{\partial z} \right ) dxdydz = 0
$$

引入哈密顿算子$\nabla$，可得微分形式如下：

$$\nabla \cdot \vec{B}=0$$

全电流定律

取空间内一点P，过P点在平行于$xOy$的平面上作一矩形闭合回路。设P处磁场强度为$H$,则距离P点$dx$处磁场强度为$H+\frac{\partial H}{\partial y} dx$，距离P点$dy$处磁场强度为$H+\frac{\partial H}{\partial x} dy$。在$xOy$平面上存在：

$$
\begin{split}
\oint_{l} \vec{H} \cdot d\vec{l} & = - \vec{H} \cdot \vec{j} \space dy + \vec{H} \cdot \vec{i} \space dx + \left ( \vec{H} + \frac{\partial \vec{H}}{\partial x} \space dx \right ) \cdot \vec{j} \space dy - \left ( \vec{H} + \frac{\partial \vec{H}}{\partial y} \space dy \right ) \cdot \vec{i} \space dx
\\
& = \left ( \frac{\partial H_y}{\partial x} - \frac{\partial H_x}{\partial y} \right ) \space dxdy
\end{split}
$$

矩形回路内包含的电流元与电通量变化率分别为：
$$
\vec{I} = \vec{J} \cdot dS = J_z \space dxdy
$$

$$
\iint_{S} \frac{\partial \vec{D}}{\partial t} \cdot d \vec{S} = \frac{\partial D_z}{\partial t} \space dxdy
$$

将以上三部分带入$\eqref{4}$式消去$dxdy$后可得：

$$
\left ( \frac{\partial H_y}{\partial x} - \frac{\partial H_x}{\partial y} \right ) = J_z + \frac{\partial D_z}{\partial t}
$$

同理对$yOz$平面和$xOz$平面进行同样的处理可得到另两个方程，综合三式可得：

$$curl \vec{H} = \vec{J} + \frac{\partial \vec{D}}{\partial t}$$

引入$\nabla$算子后可写成：

$$\nabla \times \vec{H} = \vec{J} + \frac{\partial \vec{D}}{\partial t}$$

法拉第电磁感应定律

形式与方法与全电流定律类似，同理可得：

$$curl \vec{E} = - \frac{\partial \vec{B}}{\partial t}$$

引入$\nabla$算子后可写成：

$$\nabla \times \vec{E} = -\frac{\partial \vec{B}}{\partial t}$$

总结

微分形式下的麦克斯韦方程组如下：

$$ \nabla \cdot \vec{D}=\rho \tag{1*} $$

$$ \nabla \cdot \vec{B}=0 \tag{2*} $$

$$ \nabla \times \vec{E} = -\frac{\partial \vec{B}}{\partial t} \tag{3*} $$

$$ \nabla \times \vec{H} = \vec{J} + \frac{\partial \vec{D}}{\partial t} \tag{4*} $$